Comment utiliser le cercle d’unité dans Trig

Un cercle unitaire est juste un cercle qui a un rayon d’une longueur de 1. Mais souvent, il est accompagné d’autres cloches et sifflets.

Un cercle unitaire peut être utilisé pour définir des relations de triangle rectangle appelées sinus, cosinus et tangente. Ces relations décrivent les relations entre les angles et les côtés d’un triangle rectangle. Disons, par exemple, que nous avons un triangle rectangle avec un angle de 30 degrés, et dont le côté le plus long, ou hypoténuse, a une longueur de 7. Nous pouvons utiliser nos relations de triangle rectangle prédéfinies pour déterminer les longueurs des deux côtés restants du triangle .

Cette branche des mathématiques, connue sous le nom de trigonométrie, a des applications pratiques quotidiennes telles que la construction, le GPS, la plomberie, les jeux vidéo, l’ingénierie, le travail de menuisier et la navigation aérienne.

Pour mémoriser un cercle d’unité standard, nous devons être en mesure de rappeler trois composants principaux:

Pour nous aider, nous allons rappeler un voyage à l’Unité Pizza Palace. Prenez quelques instants pour mémoriser ce qui suit jusqu’à ce que vous puissiez le réciter sans regarder:

Étape 1: 4 tranches de pizza

Imaginez une pizza entière, coupée en quatre tranches égales. En maths, nous appellerions ces quatre parties du cercle quadrants.

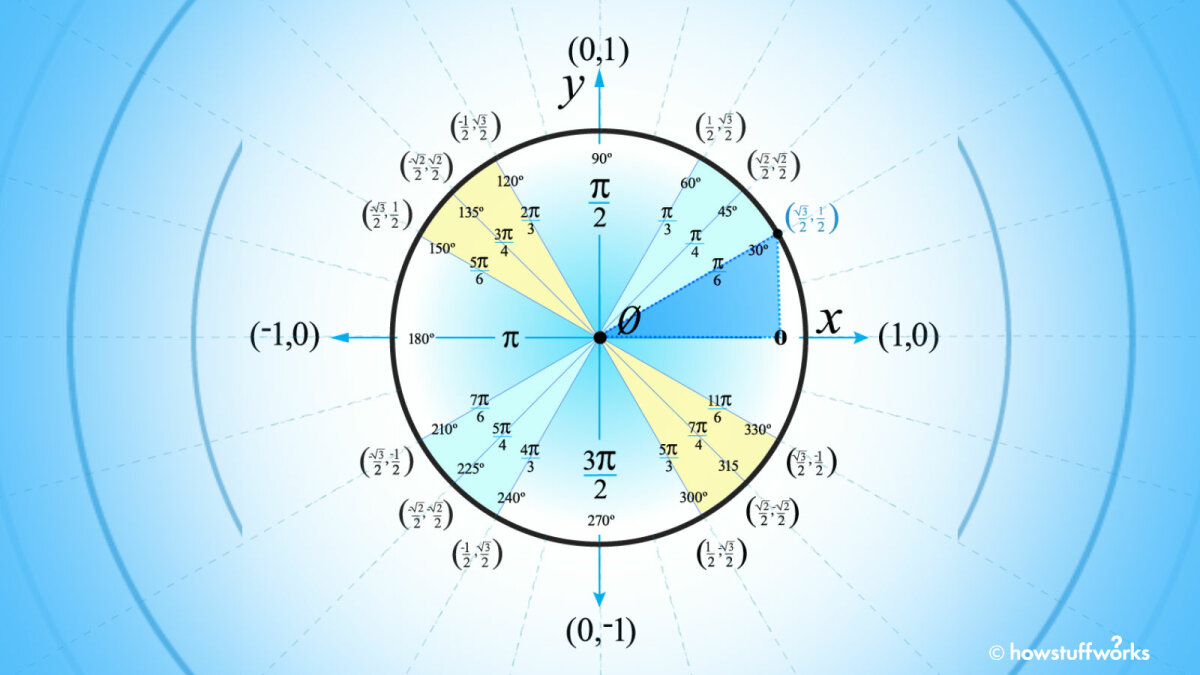
Nous pouvons utiliser les coordonnées (x, y) pour décrire n’importe quel point le long du bord extérieur du cercle. La coordonnée x représente la distance parcourue à gauche ou à droite du centre. La coordonnée y représente la distance parcourue vers le haut ou vers le bas. La coordonnée x est la cosinus de l’angle formé par le point, l’origine et l’axe des abscisses. La coordonnée y est la sinus de l’angle.

Dans un cercle unitaire, une ligne droite partant du centre du cercle atteindra le bord du cercle à la coordonnée (1, 0). Si nous montions à la place, à gauche ou à bas, nous toucherions le périmètre à (0, 1), (-1, 0) ou (0, -1) respectivement.

Les quatre angles associés (en radians et non en degrés) ont tous un dénominateur de 2. (Un radian est l’angle fait en prenant le rayon et l’enroulant autour d’un cercle. Un degré mesure les angles en fonction de la distance parcourue. Un cercle fait 360 degrés ou 2π radians).

Les numérateurs commencent à 0, commençant à la coordonnée (1,0), et comptent dans le sens inverse des aiguilles d’une montre de 1π. Ce processus donnera 0π / 2, 1π / 2, 2π / 2 et 3π / 2. Simplifiez ces fractions pour obtenir 0, π / 2, π et 3π / 2.quad

Étape 2: 3 tartes pour 6 $

Commencez par «3 tartes». Jetez un œil à l’axe y. Les angles radians directement à droite et à gauche de l’axe y ont tous un dénominateur de 3. Chaque angle restant a un numérateur qui inclut la valeur mathématique pi, écrite comme π.

“3 pies pour 6” est utilisé pour rappeler les 12 angles restants dans un cercle unitaire standard, avec trois angles dans chaque quadrant. Chacun de ces angles est écrit sous forme de fraction.

Le «pour 6 $» est de nous rappeler que dans chaque quadrant, les dénominateurs restants sont 4 puis 6.

La partie la plus délicate de cette étape consiste à compléter le numérateur pour chaque fraction.

Dans le quadrant 2 (quart supérieur gauche du cercle), mettez 2, puis 3, puis 5 devant π.

Votre premier angle dans le quadrant 2 sera 2π / 3. Additionner le 2 au numérateur et le 3 au dénominateur donnera 5. Regardez l’angle droit dans le quadrant 4 (quart inférieur droit du cercle). Placez ce 5 dans le numérateur devant π. Répétez ce processus pour les deux autres angles des quadrants 2 et 4.

Nous allons répéter le même processus pour les quadrants 1 (en haut à droite) et 3 (en bas à gauche). Rappelez-vous, tout comme x est identique à 1x, π est identique à 1π. Nous ajoutons donc 1 à tous les dénominateurs du quadrant 1.

Le processus de listage des angles en degrés (au lieu de radians) est décrit à la fin de cet article.

Étape 3: 2 tables carrées

Le “2” dans “2 tables carrées” nous rappelle que toutes les 12 paires de coordonnées restantes ont un dénominateur de 2.

«Carré» est pour nous rappeler que le numérateur de chaque coordonnée comprend une racine carrée. Nous commençons seulement par le quadrant 1 pour simplifier les choses. (Astuce: rappelez-vous que la racine carrée de 1 est 1, donc ces fractions peuvent être simplifiées à seulement 1/2.)

Étape 4: 1, 2, 3

Le “1, 2, 3” nous montre la succession des nombres sous chaque racine carrée. Pour les coordonnées x du quadrant 1, nous comptons de 1 à 3, en commençant par la coordonnée supérieure et en descendant.

Les coordonnées y ont les mêmes numérateurs, mais comptent de 1 à 3 dans la direction opposée, du bas vers le haut.

Le quadrant 2 a les mêmes coordonnées que le quadrant 1, mais les coordonnées x sont négatives.

Le quadrant 3 change les coordonnées x et y du quadrant 1. Toutes les coordonnées x et y sont également négatives.

Comme le quadrant 3, le quadrant 4 change également les coordonnées x et y du quadrant 1. Mais seules les coordonnées y sont négatives.

Angles en degrés

Vous souhaiterez peut-être référencer les angles par degrés au lieu de radians. Pour ce faire, commencez à 0 degré à la coordonnée (1,0). À partir de là, nous ajouterons 30, 15, 15 puis 30. Dans le quadrant 1, nous ajoutons 30 à 0 pour obtenir 30, 15 à 30 pour obtenir 45, 15 à 45 pour obtenir 60 et 30 à 60 pour obtenir 90.

Nous répétons ensuite le processus pour les quadrants restants, en ajoutant 30, 15, 15 et 30 jusqu’à ce que nous atteignions la fin du cercle. Le quadrant 4 aura donc des angles allant de 270 à 330 degrés (voir figure 10).

Mise en pratique

Plus tôt dans l’article, nous avons mentionné qu’un cercle unitaire pouvait être utilisé pour trouver deux côtés inconnus d’un triangle rectangle avec un angle de 30 degrés, et dont le côté le plus long, ou hypoténuse, a une longueur de 7. Essayons.

Prenez note de la position de 30 ° sur le cercle unitaire. Utilisez cette ligne et l’axe des x pour créer un triangle comme suit.

Dans un cercle unitaire, toute ligne qui commence au centre du cercle et se termine à son périmètre aura une longueur de 1. Ainsi, le côté le plus long de ce triangle aura une longueur de 1. Le côté le plus long d’un triangle rectangle est également connu sous le nom de «hypoténuse». Le point où l’hypoténuse touche le périmètre du cercle est à √3 / 2, 1/2.

On sait donc que la base du triangle (sur l’axe des x) a une longueur de √3 / 2 et la hauteur du triangle est de 1/2.

Une autre façon de penser est que la base est √3 / 2 fois la longueur de l’hypoténuse et la hauteur est 1/2 fois la longueur de l’hypoténuse.

Donc, si au contraire, l’hypoténuse a une longueur de 7, la base de notre triangle sera 7 x √3 / 2 = 7√3 / 2. La hauteur du triangle aura une longueur de 7 x 1/2 = 7/2.